Per analizzare i processi di espansione adiabatica del vapore, invece dell'approccio numerico, è possibile adottarne uno di tipo grafico che si basa sull'uso del diagramma di Mollier.
Questo diagramma concentra una moltitudine di informazioni: proprio per questo appare di una certa complessità e al primo impatto molte persone rinunciano alla sua comprensione e al suo utilizzo.
Per agevolarne la comprensione è stato scelto di mostrare la costruzione in vari passaggi di una sua versione semplificata in cui sono riportate solo le curve di interesse.
Il diagramma di Mollier è costruito sul piano H-S, cioè l'entalpia viene graficata in funzione dell'entropia.
Senza entrare nel dettaglio del significato fisico dell'entropia, non necessaria ai fini dell'utilizzo del diagramma, al lettore è sufficiente sapere che una trasformazione adiabatica (e più precisamente adiabatica reversibile) è una trasformazione di tipo isoentropico, cioè a entropia costante. Questo vuol dire che nel piano H-S l'adiabatica viene rappresentata con un tratto lineare verticale.
Per quanto concerne l'entalpia si rimanda a quanto già scritto fermo restando che per i contenuti trattati in questo post risulta di secondaria importanza. Verrà ripreso e spiegato estesamente come interpretarla al momento opportuno in altri scritti.
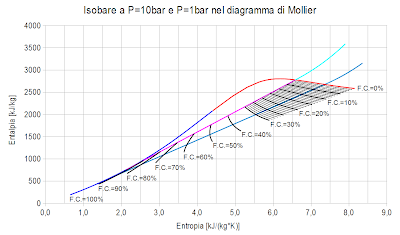
Nell'immagine che segue sono stati graficati i valori dell'entalpia in funzione dell'entropia relativi allo stato liquido e allo stato di vapore saturo.
La curva blu mostra l'andamento dello stato liquido per pressioni da 0,1bar fino alla pressione critica, la curva rossa mostra l'andamento dello stato di vapore saturo dalla pressione critica fino alla pressione di 0,1bar.
Queste due curve separano due zone del piano. Al di sopra delle curve si trovano i punti che rappresentano stati di vapore surriscaldato. Al di sotto delle curve è localizzata la zona di coesistenza del liquido con la fase di vapore saturo.
Si noti che nel punto a 0,1 bar della curva blu la frazione condensata è pari al 100%, cioè è presente la sola fase liquida.
La frazione condensata è invariata (cioè è sempre pari al 100%) per tutta l'estensione della curva blu fino al punto critico.
Nel punto critico perde di significato la distinzione fra liquido e vapore.
La curva rossa è relativa allo stato di vapore saturo in cui è assente la fase liquida: la frazione condensata è pari allo 0%.
Anche se il valore della frazione condensata nella curva del vapore è stato indicato solo nel punto in cui la pressione è pari a 0,1bar essa risulta invariata (cioè sempre pari allo 0%) per tutta l'estensione della curva rossa.
Nell'immagine che segue è stata aggiunta la curva che descrive la trasformazione isobara a 10bar che parte dallo stato liquido alla temperatura di 179,9°C (temperatura di vaporizzazione a 10bar) per arrivare allo stato di vapore surriscaldato alla pressione di 10bar e alla temperatura di 550°C.
Il tratto di curva di colore fucsia rappresenta il processo di vaporizzazione che avviene a pressione costante (10bar) e temperatura costante (179,9°C).
Quando il sistema si trova in uno dei punti di questa curva sono presenti sia il liquido che il vapore saturo. Le linee nere rappresentano stati a frazione condensata costante (il valore di quest'ultima è indicato in prossimità del punto di inizio della curva).
Il tratto di curva di colore celeste rappresenta il processo di surriscaldamento isobaro a 10bar da 179,9°C a 550°C.
Nell'immagine che segue è stata aggiunta la curva che rappresenta l'isobara alla pressione di 1bar (curva di colore blu chiaro).
Si noti che le due curve isobare scelte sono le stesse adottate negli esempi proposti per il ciclo Rankine del vapore saturo e per il ciclo Rankine del vapore surriscaldato.
Ipotizzando che lo stato di partenza dell'espansione adiabatica sia il vapore saturo a 10bar e che l'espansione adiabatica avvenga fino alla pressione di 1 bar, la trasformazione è quella rappresentata dalla linea gialla verticale.
Per stabilire la frazione condensata si valuta guardando sulle curve nere qual è il valore che più si avvicina alla intersezione fra la linea verticale gialla (adiabatica) e la curva blu chiaro (isobara a 1 bar). Cliccando sul grafico è possibile visualizzare un'immagine a risoluzione più elevata.
Si trova che il valore della frazione condensata è prossimo al 13% in perfetto accordo con quanto calcolato nel post intitolato "L'espansione adiabatica del vapore saturo - Episodio 02".
L'ultima immagine proposta è relativa ad un'espansione adiabatica in cui lo stato iniziale è il vapore a 10bar surriscaldato a 370°C.
In questo caso, l'intersezione fra la curva gialla e la curva blu chiaro avviene in corrispondenza della curva rossa: lo stato finale è quello del vapore saturo a 1bar in cui la frazione condensata è assente.
Detto in altre parole, la costruzione in figura mostra che l'espansione adiabatica del vapore da 10bar e 370°C fino a 1bar avviene senza processi di condensazione perchè il regime di saturazione viene raggiunto solo alla fine dell'espansione.
Questo diagramma concentra una moltitudine di informazioni: proprio per questo appare di una certa complessità e al primo impatto molte persone rinunciano alla sua comprensione e al suo utilizzo.
Per agevolarne la comprensione è stato scelto di mostrare la costruzione in vari passaggi di una sua versione semplificata in cui sono riportate solo le curve di interesse.
Il diagramma di Mollier è costruito sul piano H-S, cioè l'entalpia viene graficata in funzione dell'entropia.
Senza entrare nel dettaglio del significato fisico dell'entropia, non necessaria ai fini dell'utilizzo del diagramma, al lettore è sufficiente sapere che una trasformazione adiabatica (e più precisamente adiabatica reversibile) è una trasformazione di tipo isoentropico, cioè a entropia costante. Questo vuol dire che nel piano H-S l'adiabatica viene rappresentata con un tratto lineare verticale.
Per quanto concerne l'entalpia si rimanda a quanto già scritto fermo restando che per i contenuti trattati in questo post risulta di secondaria importanza. Verrà ripreso e spiegato estesamente come interpretarla al momento opportuno in altri scritti.
Nell'immagine che segue sono stati graficati i valori dell'entalpia in funzione dell'entropia relativi allo stato liquido e allo stato di vapore saturo.
La curva blu mostra l'andamento dello stato liquido per pressioni da 0,1bar fino alla pressione critica, la curva rossa mostra l'andamento dello stato di vapore saturo dalla pressione critica fino alla pressione di 0,1bar.
Queste due curve separano due zone del piano. Al di sopra delle curve si trovano i punti che rappresentano stati di vapore surriscaldato. Al di sotto delle curve è localizzata la zona di coesistenza del liquido con la fase di vapore saturo.
Si noti che nel punto a 0,1 bar della curva blu la frazione condensata è pari al 100%, cioè è presente la sola fase liquida.
La frazione condensata è invariata (cioè è sempre pari al 100%) per tutta l'estensione della curva blu fino al punto critico.
Nel punto critico perde di significato la distinzione fra liquido e vapore.
La curva rossa è relativa allo stato di vapore saturo in cui è assente la fase liquida: la frazione condensata è pari allo 0%.
Anche se il valore della frazione condensata nella curva del vapore è stato indicato solo nel punto in cui la pressione è pari a 0,1bar essa risulta invariata (cioè sempre pari allo 0%) per tutta l'estensione della curva rossa.
Nell'immagine che segue è stata aggiunta la curva che descrive la trasformazione isobara a 10bar che parte dallo stato liquido alla temperatura di 179,9°C (temperatura di vaporizzazione a 10bar) per arrivare allo stato di vapore surriscaldato alla pressione di 10bar e alla temperatura di 550°C.
Il tratto di curva di colore fucsia rappresenta il processo di vaporizzazione che avviene a pressione costante (10bar) e temperatura costante (179,9°C).
Quando il sistema si trova in uno dei punti di questa curva sono presenti sia il liquido che il vapore saturo. Le linee nere rappresentano stati a frazione condensata costante (il valore di quest'ultima è indicato in prossimità del punto di inizio della curva).
Il tratto di curva di colore celeste rappresenta il processo di surriscaldamento isobaro a 10bar da 179,9°C a 550°C.
Nell'immagine che segue è stata aggiunta la curva che rappresenta l'isobara alla pressione di 1bar (curva di colore blu chiaro).
Si noti che le due curve isobare scelte sono le stesse adottate negli esempi proposti per il ciclo Rankine del vapore saturo e per il ciclo Rankine del vapore surriscaldato.
Ipotizzando che lo stato di partenza dell'espansione adiabatica sia il vapore saturo a 10bar e che l'espansione adiabatica avvenga fino alla pressione di 1 bar, la trasformazione è quella rappresentata dalla linea gialla verticale.
Per stabilire la frazione condensata si valuta guardando sulle curve nere qual è il valore che più si avvicina alla intersezione fra la linea verticale gialla (adiabatica) e la curva blu chiaro (isobara a 1 bar). Cliccando sul grafico è possibile visualizzare un'immagine a risoluzione più elevata.
Si trova che il valore della frazione condensata è prossimo al 13% in perfetto accordo con quanto calcolato nel post intitolato "L'espansione adiabatica del vapore saturo - Episodio 02".
L'ultima immagine proposta è relativa ad un'espansione adiabatica in cui lo stato iniziale è il vapore a 10bar surriscaldato a 370°C.
In questo caso, l'intersezione fra la curva gialla e la curva blu chiaro avviene in corrispondenza della curva rossa: lo stato finale è quello del vapore saturo a 1bar in cui la frazione condensata è assente.
Detto in altre parole, la costruzione in figura mostra che l'espansione adiabatica del vapore da 10bar e 370°C fino a 1bar avviene senza processi di condensazione perchè il regime di saturazione viene raggiunto solo alla fine dell'espansione.







Yuz,
RispondiEliminauna semplice curiosità: la lunghezza della linea gialla, che mostra un'espansione iso-entropica, quindi adiabatica reversibile, che cosa esprime dal punto di visto termodinamico?
La lunghezza della linea gialla si esprime matematicamente come differenza fra il valore dell'entalpia nel punto iniziale (quello in alto) e il valore dell'entalpia nel punto finale (quello in basso).
EliminaTale valore rappresenta il lavoro utile di un ipotetico ciclo Rankine e costituisce pertanto il massimo lavoro teorico ottenibile usando vapore a quelle condizioni operative.
Grazie Yuz,
RispondiEliminamolto semplice per calcolare il massimo lavoro ottenibile, avendo a disposizione il diagramma di Mollier.
Ma se dovessi calcolare il rendimento del ciclo Rankine ideale, come si fa col diagramma di Mollier?
E' altrettanto semplice?
Certamente, il calcolo del rendimento è altrettanto semplice.
EliminaIl calore fornito è pari alla differenza fra il valore dell'entalpia all'inizio dell'espansione adiabatica (punto più alto della linea gialla) e il valore dell'entalpia dello stato liquido (F.C. = 100%) alla temperatura di condensazione (punto più a sinistra della linea blu chiaro). Purtroppo nel grafico del post questo punto non si distingue molto chiaramente. Il valore esatto dell'entalpia è 418 kJ/kg.
Il rendimento dell'ipotetico ciclo Rankine è dato dal rapporto fra il lavoro utile (lunghezza della linea gialla) e il calore fornito appena calcolato.
Sì, il grafico è poco chiaro perchè in quel tratto è tutto compresso, ma se i dati da cui lo si ricava sono tutti tabellati, è un gioco da ragazzi fare il calcolo...
RispondiEliminaHo un'alimentazione costituita da vapore saturo a 42 bar (Ts=253°C) e da etilbenzene a 2 bar e 136°C.
RispondiEliminaIl vapore saturo viene surriscaldato mentre l'etilbenzene liquido viene riscaldato.
Dopo la loro miscelazione, vengono fatti entrare in un reattore adiabatico che opera a 1.6 bar e 560°C.
La domanda è la seguente:conviene far compiere al vapore saturo un'espansione in valvola oppure fornirgli calore e poi dopo la miscelazione con l'etilbenzene compiere l'espansione?
Ciao Luca e benvenuto su Scienza Laterale.
EliminaDovresti darmi qualche chiarimento sul problema che proponi.
Scrivi:
Ho un'alimentazione costituita da vapore saturo a 42 bar (Ts=253°C) e da etilbenzene a 2 bar e 136°C.
L'etilbenzene a 136°C e 2 bar è in fase liquida. L'alimentazione è costituita da vapore acqueo miscelato con etilbenzene liquido?
I due fluidi sono a diversa temperatura quindi nella miscelazione le temperature cambiano.
Qual è il rapporto di massa fra le due sostanze?
Il vapore saturo viene surriscaldato mentre l'etilbenzene liquido viene riscaldato.
Se ti stai riferendo alla miscelazione, il vapore saturo si raffredda e tende a condensare, mentre l'etilbenzene si riscalda e tende a vaporizzare.
Oppure il surriscaldamento del vapore è un processo a parte?
Dopo la loro miscelazione, vengono fatti entrare in un reattore adiabatico che opera a 1.6 bar e 560°C.
La domanda è la seguente:conviene far compiere al vapore saturo un'espansione in valvola oppure fornirgli calore e poi dopo la miscelazione con l'etilbenzene compiere l'espansione?
Riesci ad aggiugere qualche dettaglio in più?
Quando parli di reattore intendi un espansore per estrarre lavoro meccanico oppure un contenitore a volume fisso dove avverrà una reazione chimica?
I 560°C di temperatura mi fanno propendere per la seconda opzione.
ciao, avrei un dubbio circa la pendenza delle rette isoterme e isobare. Perchè il coefficiente angolare aumenta all'aumentare della temperatura? il libro poi mi dice che fissata una temperatura di saturazione la pendenza delle isoterme ( e delle isobare) all'interno della campana di Andrews è uguale a quella della curva limite inferiore in quel punto..perchè? grazie
RispondiEliminaCiao Dujan51 e benvenuto su Scienza Laterale.
EliminaAll'interno della campana di Andrews si ha la coesistenza della fase vapore e di quella liquida.
In questo caso entalpia ed entropia sono date dalle equazioni:
H = FC * Hliq + FV * Hvap = FC * Hliq + ( 1- FC) * Hvap
S = FC * Sliq + FV * Svap = FC * Sliq + ( 1- FC) * Svap
in cui
FC è la frazione condensata
FV è la frazione vaporizzata
Hliq è l'entalpia del liquido saturo
Hvap è l'entalpia del vapore saturo
Sliq è l'entropia del liquido saturo
Svap è l'entropia del vapore saturo
Eliminando la variabile FC fra le due equazioni e facendo alcuni passaggi algebrici è possibile ricavare l'equazione di H in funzione S.
Tale equazione è di tipo lineare con coefficiente angolare m pari a
m = ( Hvap - Hliq) / ( Svap - Sliq )
La risposta sul perchè il coefficiente angolare all'interno della campana di Andrews aumenta all'aumentare della temperatura è nell'equazione sopra.
il libro poi mi dice che fissata una temperatura di saturazione la pendenza delle isoterme ( e delle isobare) all'interno della campana di Andrews è uguale a quella della curva limite inferiore in quel punto
Anche se non capisco cosa intenda il tuo libro con curva limite, immagino che si riferisca alla continuità dell'isobara quando attraversa la linea rossa nei grafici mostrati in questo post.
sempre nel grafico h-s
RispondiEliminaintende la linea di separazione fra la regione bifasica e la fase liquida. Grazie mille. Avrei però ancora qualche dubbio.Cioè m aumenta perchè (Svap - Sliq) è sempre positivo, l'entalpia è funzione della temperatura e l'entalpia del vapore è maggiore dell'entalpia del liquido? non mi è molto chiaro questo aspetto. Inoltre, nell'equazione iniziale, il raccoglimento a (1-FC)Hvap. La FC di Hvap è diversa quindi da Hliq? ho un po' di confusione su questi concetti, grazie
RispondiEliminaInoltre, nell'equazione iniziale, il raccoglimento a (1-FC)Hvap.
EliminaNon si tratta di un raccoglimento, bensì di una sostituzione, in quanto si sfrutta la proprietà FC + FV = 1.
Cioè m aumenta perchè (Svap - Sliq) è sempre positivo, l'entalpia è funzione della temperatura e l'entalpia del vapore è maggiore dell'entalpia del liquido?
Riporto per comodità l'equazione per il coefficiente angolare m
m = ( Hvap - Hliq) / ( Svap - Sliq )
Il coefficiente m è sempre positivo perchè numeratore e denominatore nella relativa equazione sono sempre positivi in quanto
Svap > Sliq
Hvap > Hliq
Vediamo perchè.
Per individuare come variano le grandezze fisiche coinvolte conviene riferirsi alla prima figura del post, quella con la linea rossa e la linea blu.
La linea rossa è relativa allo stato di vapore saturo (FC=0, FV=1), quella blu è relativa allo stato di liquido saturo (FC=1, FV=0).
Osserva che:
1) La curva rossa è posizionata interamente a destra rispetto alla curva blu (cioè lo stato vapore è SEMPRE a maggiore ENTROPIA dello stato liquido): Svap > Sliq
2) La curva rossa è posizionata interamente sopra alla curva blu (cioè lo stato vapore è SEMPRE a maggiore ENTALPIA dello stato liquido): Hvap > Hliq
La zona delle basse pressioni si trova sull'estremità a sinistra nel caso della linea blu, sull'estremità destra nel caso della linea rossa. All'aumentare della pressione ci si sposta verso il centro e le due linee si toccano al raggiungimento della pressione critica.
La pendenza della curva blu (che è quella del liquido saturo) è maggiore di quella rossa (che è quella del vapore saturo).
Questo significa che all'aumentare della pressione (e quindi della temperatura di vaporizzazione) il termine al denominatore Hvap - Hliq diminuisce più rapidamente del termine al numeratore Svap - Sliq e quindi il valore del coefficiente angolare m aumenta.
inoltre mi piacerebbe sapere, il fatto che la pendenza delle isocore sia maggiore di quella delle isobare, cosa comporta dal punto di vista termodinamico? cioè, mi conviene fare una trasformazione isobara diminuendo l'area sottesa? cosa rappresenta quell'area? grazie
RispondiEliminaAnche se nel blog non ho mai presentato diagrammi di Mollier con trasformazioni isocore, provo comunque a darti qualche dritta.
EliminaCome dici tu, l'isocora ha effettivamente una maggiore pendenza dell'isobara nel piano H-S.
Il confronto che hai in mente è però improprio in quanto una trasformazione isocora e una trasformazione isobara che iniziano nello stesso stato finiscono sempre con due stati fisici distinti.
L'area sottesa dalle curve di trasformazione nel piano H-S non mi risulta che abbia alcun significato fisico preciso.
ok, grazie Yuz! L'ultima cosa che non ho capito riguardo al post precedente è: "La pendenza della curva blu (che è quella del liquido saturo) è maggiore di quella rossa (che è quella del vapore saturo).
RispondiEliminaQuesto significa che all'aumentare della pressione (e quindi della temperatura di vaporizzazione) il termine al denominatore Hvap - Hliq diminuisce più rapidamente del termine al numeratore Svap - Sliq e quindi il valore del coefficiente angolare m aumenta.". Hvap-Hliq perchè al denominatore in contrasto con l'equazione m = ( Hvap - Hliq) / ( Svap - Sliq) ?
Rileggendo la frase, mi sono reso conto di aver scritto un'idiozia.
EliminaE' esattamente il contrario.
Il termine Hvap - Hliq (numeratore) diminuisce meno rapidamente del termine Svap - Sliq (denominatore).
Ok grazie! Le trasformazioni isocore terminano sempre in stati fisici diversi rispetto alle isobare partendo dallo stesso stadio? In ogni caso?
RispondiEliminaA me risulta che sia così, ma se riesci a portarmi un esempio che mi smentisca sono pronto a cambiare opinione.
EliminaSalve,
RispondiEliminaPer quale motivo nel piano di Mollier il punto critico non si trova nel punto più alto della curva ?
Ciao Giuseppe,
Eliminabenvenuto sul blog.
Non è facile rispondere alla tua domanda.
Volendo azzardare una risposta, credo che in prossimità del punto critico lo stato di vapore abbia caratteristiche più simili a un liquido che a un gas. Questo significa che il passaggio di stato risulta meno oneroso dal punto di vista energetico.