Per quanto già trattato, il rendimento del ciclo Brayton può essere valutato utilizzando la seguente relazione
Rendimento = 1 - (Pminima/Pmassima)[ (gamma - 1) / gamma ]
La formula necessita però di alcune indicazioni per l'uso perchè altrimenti induce a delle conclusioni errate.
Dal punto di vista algebrico il rapporto Pminima/Pmassima può assumere un qualunque valore compreso fra 0 e 1.
Il rapporto vale 1 quando Pminima = Pmassima e si riduce progressivamente a 0 al crescere di Pmassima (o anche al diminuire di Pminima).
In figura è stato stato graficato l'andamento del rendimento in funzione di Pminima/Pmassima per i tre tipi di gas.
Le curve mostrano che il rendimento aumenta al diminuire del rapporto Pminima/Pmassima.
In pratica, a parità di Pminima, aumentare Pmassima significa ottenere rendimenti migliori.
I grafici confermano la considerazione già fatta in precendenza che il miglior rendimento si ha con il gas monoatomico, poi con quello biatomico e a seguire con il poliatomico.
La formula fa erroneamente ritenere accessibili rendimenti prossimi al 100% o almeno di rendere possibili rendimenti superiori a quello di Carnot.
Nessuna delle due possibilità corrisponde a verità.
Vediamo cosa accade al ciclo di Brayton vincolando alcuni parametri operativi e facendo variare esclusivamente il rapporto di pressioni Pminima/Pmassima.
Prendiamo come riferimento i parametri utilizzati nell'esempio presentato alla fine del precedente post, e consideriamo costanti
TA = 300K
TC = 600K
VD = 3m3
Pminima = 100kPa
Di seguito sono raccolti nello stesso diagramma PV i cicli di Brayton a diversi rapporti di pressione.
Nel grafico si passa da una situazione estrema in cui
Pminima/Pmassima = 1
che è rappresentata dal tratto orizzontale a P = 100kPa (assenza delle trasformazioni adiabatiche e presenza di due trasformazioni isobare sovrapposte) ad un'altra situazione estrema in cui
Pmassima = 550kPa
che viene rappresentata dalla linea curva di colore marrone (assenza delle trasformazioni isobare e presenza di due trasformazioni adiabatiche sovrapposte).
Fra queste due situazioni estreme, tre posizioni intermedie in cui è presente il classico ciclo di Brayton.
Il ciclo azzurro che si trova al di sopra della curva marrone è sempre un ciclo Brayton ma sostanzialmente diverso precedenti: il lavoro utile di questo ciclo è negativo.
Si tratta cioè di un esempio in cui il ciclo di Brayton funge da pompa di calore e non da motore termico.
La formula che calcola il rendimento del ciclo Brayton in funzione del rapporto Pminima / Pmassima è valida fintantochè il valore di Pminima / Pmassima è maggiore del valore a cui si osserva la scomparsa delle trasformazioni isobare.
Tale valore limite dipende dalle condizioni operative e dal tipo di gas.
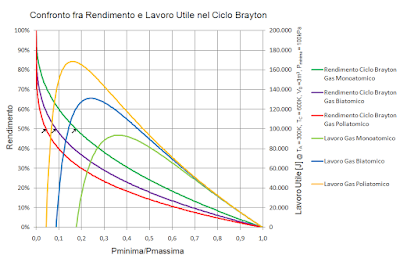
Per chiarire il concetto, consideriamo un grafico che presenta assieme rendimento e lavoro utile per i tre tipi di gas.
La figura permette di fare alcune importanti considerazioni.
Il lavoro utile ha un andamento diverso da quello del rendimento.
Ha valore nullo quando il rapporto di pressioni ha un valore unitario e aumenta progressivamente fino ad un massimo al diminuire del rapporto di pressioni.
Il valore del rapporto di pressioni a cui corrisponde il massimo del lavoro utile è maggiore del punto in cui avviene la scomparsa delle isobare.
Oltre il massimo, riducendo ancora il rapporto di pressione, il lavoro utile diminuisce rapidamente fino ad annullarsi al raggiungimento del valore del rapporto di pressioni a cui scompaiono le isobare.
E' curioso che la formula del rendimento applicata al caso del ciclo Brayton in cui sono assenti le isobare fornisce come risultato il rendimento di Carnot
Rendimento = 1 - (Pminima/Pmassima)[ (gamma - 1) / gamma ] = 1 - TA / TC
Si noti che nel grafico sono presenti tre frecce nere che indicano il punto delle tre curve di rendimento in cui viene raggiunto il 50% (che è pari al rendimento di Carnot alle condizioni operative considerate per l'analisi eseguita in questo post).
DIMOSTRAZIONE
Poichè il ciclo è composto da due adiabatiche sovrapposte vale
Pminima*VDgamma = Pminima*VAgamma = Pmassima*VCgamma = Pmassima*VBgamma
Pminima*VAgamma = Pmassima*VCgamma
VCgamma / VAgamma = Pminima/Pmassima
(VC / VA)gamma = Pminima/Pmassima
VC / VA = (Pminima/Pmassima)1/gamma
Inoltre
Pminima*VAgamma = Pmassima*VCgamma
Pminima*VA*VA(gamma - 1) = Pmassima*VC*VC(gamma - 1)
n*R*TA*VA(gamma - 1) = n*R*TC*VC(gamma - 1)
TA*VA(gamma - 1) = TC*VC(gamma - 1)
TA/TC = VC(gamma - 1) / VA(gamma - 1) = (VC / VA)(gamma - 1)
Per quanto visto sopra
VC / VA = (Pminima/Pmassima)1/gamma
quindi
TA/TC = [(Pminima/Pmassima)1/gamma](gamma - 1) = (Pminima/Pmassima)[ (gamma - 1) / gamma ]
Sostituendo quest'ultima relazione in quella per il rendimento si ottiene
Rendimento = 1 - TA / TC
che è il rendimento di Carnot dal momento che TA e TC sono rispettivamente le temperature minima e massima del ciclo.
Rendimento = 1 - (Pminima/Pmassima)[ (gamma - 1) / gamma ]
La formula necessita però di alcune indicazioni per l'uso perchè altrimenti induce a delle conclusioni errate.
Dal punto di vista algebrico il rapporto Pminima/Pmassima può assumere un qualunque valore compreso fra 0 e 1.
Il rapporto vale 1 quando Pminima = Pmassima e si riduce progressivamente a 0 al crescere di Pmassima (o anche al diminuire di Pminima).
In figura è stato stato graficato l'andamento del rendimento in funzione di Pminima/Pmassima per i tre tipi di gas.
Le curve mostrano che il rendimento aumenta al diminuire del rapporto Pminima/Pmassima.
In pratica, a parità di Pminima, aumentare Pmassima significa ottenere rendimenti migliori.
I grafici confermano la considerazione già fatta in precendenza che il miglior rendimento si ha con il gas monoatomico, poi con quello biatomico e a seguire con il poliatomico.
La formula fa erroneamente ritenere accessibili rendimenti prossimi al 100% o almeno di rendere possibili rendimenti superiori a quello di Carnot.
Nessuna delle due possibilità corrisponde a verità.
Vediamo cosa accade al ciclo di Brayton vincolando alcuni parametri operativi e facendo variare esclusivamente il rapporto di pressioni Pminima/Pmassima.
Prendiamo come riferimento i parametri utilizzati nell'esempio presentato alla fine del precedente post, e consideriamo costanti
TA = 300K
TC = 600K
VD = 3m3
Pminima = 100kPa
Di seguito sono raccolti nello stesso diagramma PV i cicli di Brayton a diversi rapporti di pressione.
Nel grafico si passa da una situazione estrema in cui
Pminima/Pmassima = 1
che è rappresentata dal tratto orizzontale a P = 100kPa (assenza delle trasformazioni adiabatiche e presenza di due trasformazioni isobare sovrapposte) ad un'altra situazione estrema in cui
Pmassima = 550kPa
che viene rappresentata dalla linea curva di colore marrone (assenza delle trasformazioni isobare e presenza di due trasformazioni adiabatiche sovrapposte).
Fra queste due situazioni estreme, tre posizioni intermedie in cui è presente il classico ciclo di Brayton.
Il ciclo azzurro che si trova al di sopra della curva marrone è sempre un ciclo Brayton ma sostanzialmente diverso precedenti: il lavoro utile di questo ciclo è negativo.
Si tratta cioè di un esempio in cui il ciclo di Brayton funge da pompa di calore e non da motore termico.
La formula che calcola il rendimento del ciclo Brayton in funzione del rapporto Pminima / Pmassima è valida fintantochè il valore di Pminima / Pmassima è maggiore del valore a cui si osserva la scomparsa delle trasformazioni isobare.
Tale valore limite dipende dalle condizioni operative e dal tipo di gas.
Per chiarire il concetto, consideriamo un grafico che presenta assieme rendimento e lavoro utile per i tre tipi di gas.
La figura permette di fare alcune importanti considerazioni.
Il lavoro utile ha un andamento diverso da quello del rendimento.
Ha valore nullo quando il rapporto di pressioni ha un valore unitario e aumenta progressivamente fino ad un massimo al diminuire del rapporto di pressioni.
Il valore del rapporto di pressioni a cui corrisponde il massimo del lavoro utile è maggiore del punto in cui avviene la scomparsa delle isobare.
Oltre il massimo, riducendo ancora il rapporto di pressione, il lavoro utile diminuisce rapidamente fino ad annullarsi al raggiungimento del valore del rapporto di pressioni a cui scompaiono le isobare.
E' curioso che la formula del rendimento applicata al caso del ciclo Brayton in cui sono assenti le isobare fornisce come risultato il rendimento di Carnot
Rendimento = 1 - (Pminima/Pmassima)[ (gamma - 1) / gamma ] = 1 - TA / TC
Si noti che nel grafico sono presenti tre frecce nere che indicano il punto delle tre curve di rendimento in cui viene raggiunto il 50% (che è pari al rendimento di Carnot alle condizioni operative considerate per l'analisi eseguita in questo post).
DIMOSTRAZIONE
Poichè il ciclo è composto da due adiabatiche sovrapposte vale
Pminima*VDgamma = Pminima*VAgamma = Pmassima*VCgamma = Pmassima*VBgamma
Pminima*VAgamma = Pmassima*VCgamma
VCgamma / VAgamma = Pminima/Pmassima
(VC / VA)gamma = Pminima/Pmassima
VC / VA = (Pminima/Pmassima)1/gamma
Inoltre
Pminima*VAgamma = Pmassima*VCgamma
Pminima*VA*VA(gamma - 1) = Pmassima*VC*VC(gamma - 1)
n*R*TA*VA(gamma - 1) = n*R*TC*VC(gamma - 1)
TA*VA(gamma - 1) = TC*VC(gamma - 1)
TA/TC = VC(gamma - 1) / VA(gamma - 1) = (VC / VA)(gamma - 1)
Per quanto visto sopra
VC / VA = (Pminima/Pmassima)1/gamma
quindi
TA/TC = [(Pminima/Pmassima)1/gamma](gamma - 1) = (Pminima/Pmassima)[ (gamma - 1) / gamma ]
Sostituendo quest'ultima relazione in quella per il rendimento si ottiene
Rendimento = 1 - TA / TC
che è il rendimento di Carnot dal momento che TA e TC sono rispettivamente le temperature minima e massima del ciclo.
APPROFONDIMENTI CONSIGLIATI
Sullo stesso argomento si segnala la discussione intitolata "Ragionamenti sul ciclo di Brayton-Joule" presente sul forum Scienza Laterale.
Sullo stesso argomento si segnala la discussione intitolata "Ragionamenti sul ciclo di Brayton-Joule" presente sul forum Scienza Laterale.






Nessun commento:
Posta un commento
Puoi scrivere qui eventuali richieste di chiarimenti, perplessità o il tuo parere su quanto esposto / Please, write here questions, doubts or your opinion on the post