La seconda modifica introdotta nel precedente post, cioè l'aggiunta del collegamento a U che consente lo scarico di gas freddo e la completa rigenerazione termica, ha permesso di migliorare sensibilmente il rendimento del motore di Cayley free piston.
L'efficienza termomeccanica è salita al 32,5% ed è indipendente dal tipo di gas.
Forse è passato inosservato che le valutazioni fatte fino a questo punto sono state riferite al caso particolare in cui il rapporto fra superficie del pistone caldo e superficie del pistone freddo è pari a 1,5.
Abbiamo già visto che per il funzionamento di questo motore bisogna rispettare il vincolo
Scalda / Sfredda < Tcalda / Tfredda
in cui
Scalda è la superficie del pistone caldo espressa in m2
Sfredda è la superficie del pistone freddo espressa in m2
Tcalda è la temperatura del cilindro caldo espressa in K
Tfredda è la temperatura del cilindro freddo espressa in K
Poichè le temperature operative adottate per l'analisi erano
Tcalda = 600K
Tfredda = 300K
un qualunque valore compreso fra 1 e Tcalda/Tfredda = 600K/300K = 2 sarebbe stato accettabile.
La scelta di utilizzare il valore di 1,5 per le valutazioni non è stata casuale: in questo post ne scopriremo il motivo.
Come prima cosa consideriamo i due casi estremi: Scalda/Sfredda = 1 e Scalda/Sfredda = 2.
Quando Scalda/Sfredda = 1 il gas compie una trasformazione isocora.
Il lavoro è nullo perchè non c'è variazione di volume.
Nel secondo caso, quando il rapporto fra le superfici vale 2, ovvero quando uguaglia il rapporto delle temperature, l'area del ciclo scompare (il lavoro utile si annulla) e il gas compie una trasformazione isobara con la stessa pressione sia all'andata che al ritorno.
All'apertura delle valvole non accade nulla perchè non c'è differenza di pressione fra l'interno e l'esterno del motore.
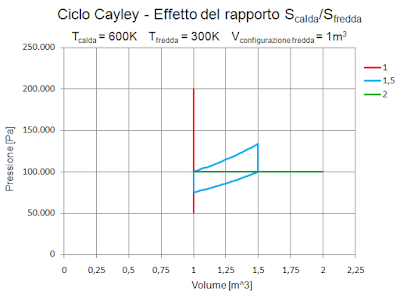
Il diagramma P-V aiuta meglio a chiarire il concetto.
Nel grafico il tratto verticale di colore rosso rappresenta il caso isocoro (Scalda/Sfredda = 1) e il tratto orizzontale di colore verde il caso isobaro (Scalda/Sfredda = 2).
Per completezza è stato riportato in colore azzurro anche il ciclo di Cayley analizzato nei precedenti episodi (Scalda/Sfredda = 1,5).
Ora vediamo cosa accade al ciclo quando i valori di Scalda/Sfredda sono compresi fra 1 e 2.
Nel grafico sono riportati i cicli relativi a rapporti fra le superfici che vanno da 1 a 2 per salti di 0,1.
I grafici in figura mostrano che all'aumentare del rapporto fra le superfici, diminuisce la pressione massima e aumenta la pressione minima. Abbiamo già detto che quando Scalda/Sfredda è pari a 2 la pressione massima uguaglia la pressione minima.
Nel grafico che segue sono riportati gli andamenti del rendimento e del lavoro utile in funzione del rapporto Scalda/Sfredda.
L'efficienza termomeccanica è salita al 32,5% ed è indipendente dal tipo di gas.
Forse è passato inosservato che le valutazioni fatte fino a questo punto sono state riferite al caso particolare in cui il rapporto fra superficie del pistone caldo e superficie del pistone freddo è pari a 1,5.
Abbiamo già visto che per il funzionamento di questo motore bisogna rispettare il vincolo
Scalda / Sfredda < Tcalda / Tfredda
in cui
Scalda è la superficie del pistone caldo espressa in m2
Sfredda è la superficie del pistone freddo espressa in m2
Tcalda è la temperatura del cilindro caldo espressa in K
Tfredda è la temperatura del cilindro freddo espressa in K
Poichè le temperature operative adottate per l'analisi erano
Tcalda = 600K
Tfredda = 300K
un qualunque valore compreso fra 1 e Tcalda/Tfredda = 600K/300K = 2 sarebbe stato accettabile.
La scelta di utilizzare il valore di 1,5 per le valutazioni non è stata casuale: in questo post ne scopriremo il motivo.
Come prima cosa consideriamo i due casi estremi: Scalda/Sfredda = 1 e Scalda/Sfredda = 2.
Quando Scalda/Sfredda = 1 il gas compie una trasformazione isocora.
Il lavoro è nullo perchè non c'è variazione di volume.
Nel secondo caso, quando il rapporto fra le superfici vale 2, ovvero quando uguaglia il rapporto delle temperature, l'area del ciclo scompare (il lavoro utile si annulla) e il gas compie una trasformazione isobara con la stessa pressione sia all'andata che al ritorno.
All'apertura delle valvole non accade nulla perchè non c'è differenza di pressione fra l'interno e l'esterno del motore.
Il diagramma P-V aiuta meglio a chiarire il concetto.
Nel grafico il tratto verticale di colore rosso rappresenta il caso isocoro (Scalda/Sfredda = 1) e il tratto orizzontale di colore verde il caso isobaro (Scalda/Sfredda = 2).
Per completezza è stato riportato in colore azzurro anche il ciclo di Cayley analizzato nei precedenti episodi (Scalda/Sfredda = 1,5).
Ora vediamo cosa accade al ciclo quando i valori di Scalda/Sfredda sono compresi fra 1 e 2.
Nel grafico sono riportati i cicli relativi a rapporti fra le superfici che vanno da 1 a 2 per salti di 0,1.
I grafici in figura mostrano che all'aumentare del rapporto fra le superfici, diminuisce la pressione massima e aumenta la pressione minima. Abbiamo già detto che quando Scalda/Sfredda è pari a 2 la pressione massima uguaglia la pressione minima.
Nel grafico che segue sono riportati gli andamenti del rendimento e del lavoro utile in funzione del rapporto Scalda/Sfredda.
Il grafico mostra due cose estremamente importanti.
La prima è che il rendimento è nullo quando Scalda/Sfredda = 1.
La seconda è che il rendimento migliora all'aumentare del rapporto Scalda/Sfredda e al limite uguaglia quello di Carnot (pari al 50% alle temperature adottate) quando Scalda/Sfredda = Tcalda/Tfredda.
Il lavoro utile ha invece un andamento crescente per Scalda/Sfredda che varia da 0 fino a circa 1,45 e decrescente fino ad annullarsi per Scalda/Sfredda che varia da 1,45 a 2. L'annullamento del lavoro utile al raggiungimento del rendimento di Carnot è una caratteristica che il ciclo Cayley ha in comune con il ciclo Brayton.
Nei calcoli dei precedenti episodi è stato adottato il valore di Scalda/Sfredda pari a 1,5 per massimizzare il lavoro utile.
Perchè se da un lato è importante il rendimento, dall'altro è fondamentale che il motore sviluppi una potenza specifica significativa: un motore che sviluppa un basso lavoro utile potrebbe perfino non muoversi perchè non riesce a vincere gli attriti fra le sue parti mobili.
In questo post è stato mostrato che con il motore Cayley è possibile incrementare il rendimento fino a valori estremamente elevati spingendo il rapporto Scalda/Sfredda a valori prossimi a Tcalda/Tfredda.
Va comunque sempre tenuto presente che avvicinarsi a tale limite comporta sempre una perdita di potenza specifica.
Nel prossimo post verrà aggiunto un altro tassello per comprendere più a fondo le potenzialità di questo motore.
La prima è che il rendimento è nullo quando Scalda/Sfredda = 1.
La seconda è che il rendimento migliora all'aumentare del rapporto Scalda/Sfredda e al limite uguaglia quello di Carnot (pari al 50% alle temperature adottate) quando Scalda/Sfredda = Tcalda/Tfredda.
Il lavoro utile ha invece un andamento crescente per Scalda/Sfredda che varia da 0 fino a circa 1,45 e decrescente fino ad annullarsi per Scalda/Sfredda che varia da 1,45 a 2. L'annullamento del lavoro utile al raggiungimento del rendimento di Carnot è una caratteristica che il ciclo Cayley ha in comune con il ciclo Brayton.
Nei calcoli dei precedenti episodi è stato adottato il valore di Scalda/Sfredda pari a 1,5 per massimizzare il lavoro utile.
Perchè se da un lato è importante il rendimento, dall'altro è fondamentale che il motore sviluppi una potenza specifica significativa: un motore che sviluppa un basso lavoro utile potrebbe perfino non muoversi perchè non riesce a vincere gli attriti fra le sue parti mobili.
In questo post è stato mostrato che con il motore Cayley è possibile incrementare il rendimento fino a valori estremamente elevati spingendo il rapporto Scalda/Sfredda a valori prossimi a Tcalda/Tfredda.
Va comunque sempre tenuto presente che avvicinarsi a tale limite comporta sempre una perdita di potenza specifica.
Nel prossimo post verrà aggiunto un altro tassello per comprendere più a fondo le potenzialità di questo motore.